Any two cords that intersect within the same circle will create two equal area rectangles if you multiply the two segments of the. Cosθ 2 sinθ 2 1 a useful identity Important Angles.

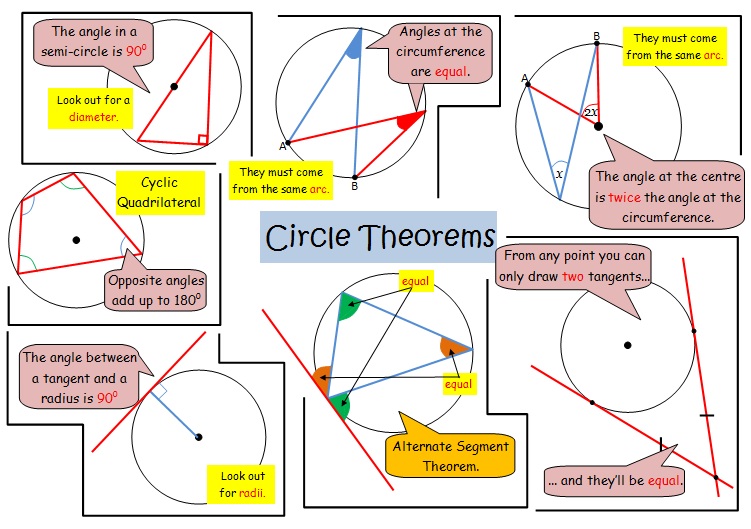
Circle Theorems Angles At Centre Circumference Cie Igcse Maths Revision Notes
Circle Thereom Rules Note
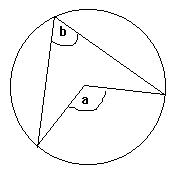
Circle Theorems Mathematics Gcse Revision
It has truly earth-shattering implications.

Circle theorem rules. Thales established what has become known as Thales Theorem whereby if a triangle is drawn within a circle with the long side as a diameter of the circle. The three sides of a right-angled triangle have specific names. The 1 Mathematical Discovery of the 20th Century In 1931 the young mathematician Kurt Gödel made a landmark discovery as powerful as anything Albert Einstein developed.
This theorem should be self-explanatory form its nametitle. In other words just like for the exponentiation of numbers ie 𝑎 𝑎 𝑎 the square is obtained by multiplying the matrix by itself. In short it seems that is behaving in a similar fashion to.
They could for example easily trisect an. C 2 π1 2 π. Fundamental Theorem of Algebra.
A circle graph or a pie chart is used to visualize information and data. We will develop the Pythagorean Theorem and use it to solve for the missing side length of a right. BD is a diameter of the circle we know that triangle BAD is confined within the semi-circle.
There are 4 common rules for solving a triangle as explained below. You can divide a circle into smaller portions. Trigonometry involves calculating angles and sides in triangles.
That is using repeated observations to establish rules of thumb. 30 45 and 60. Frequency of Periodic Motion.
The circumference of the unit circle is. The interactive demonstration below shows that the sum of the lengths of any 2 sides of a triangle must exceed the length of the third side. A circle is a shape consisting of all points in a plane that are at a given distance from a given point the centre.
Squaring the circle is a problem proposed by ancient geometersIt is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedgeThe difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square. Frustum of a Cone or Pyramid. We just convinced you this limit formula holds true based on the graph but how does one attempt to prove this limit more formally.
The semicircle arises if you ignore the right-hand side of the diameter in the diagram above. Circumcenter of a triangle Opens a modal Circumcenter of a right triangle Opens a modal Three points defining a circle Opens a modal Area circumradius formula proof Opens a modal 2003 AIME II problem. As one might notice the most basic requirement for matrix exponentiation to be defined is that 𝐴 must be square.
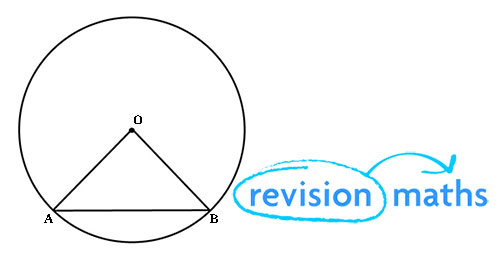
Aside from the basic formula of side x height we have the SSS ASA SAS and SSA rules for solving a triangle where S is a side length and A is the angle in degrees. Two Radii and a chord make an isosceles triangle. Graph of SineCosine from Unit Circle.
Law of Sines and Cosines. How to use the pythagorean Theorem Surface area of a Cylinder Unit Circle Game Pascals Triangle demonstration Create save share charts Interactive. The first 3 circle theorems.
This is because for two general matrices 𝐴 and 𝐵 the matrix multiplication 𝐴 𝐵 is only well defined if there is the. That is when we divide px by x-a we obtain. The First Fundamental Theorem of Calculus.
X 2 y 2 1 equation of the unit circle. Theorem functions on an actual case that a polynomial is comprehensively dividable at least one time by its factor in order to get a smaller polynomial and a remainder of zero. A part of a circle is called an arc and an arc is named according to its angle.
Gödels discovery not only applied to mathematics but literally all branches of science logic and human knowledge. Frequency of a Periodic Function. To do this we need to be quite clever and to employ some indirect reasoning.
This acts as one of the simplest ways to determine whether the value a is a root of the polynomial Px. Ambiguous Case Law of Sines. More trig gifs.
Triangle inequality theorem Opens a modal Practice. Circle terminology and construction and applications of circles in the. Area of a Triangle calculation.
We solve examples and highlight rules for performing calculations without using a. The hypotenuse h. Pythagoras Theorem says that for a right angled triangle the square of the long side equals the sum of the squares of the other two sides.
But 1 2 is just 1 so. S o if a point starts at 1 0 and moves counterclockwise all the way around the unit circle and returns to 1 0 it travels a distance of 2 πTo move halfway around the circle it travels a distance of 122 π π. Triangle side length rules.
A right triangle consists of two legs and a hypotenuse. The angle at the circumference in a semicircle is a right angle. The diagram below shows that to find the reference number t its helpful to know the quadrant in which the terminal point determined by t lies.
To move a quarter of the distance around the circle it travels a distance of 142 π π2. If a question says show our workings you must state what circle theoremgeometry fact you use when you use it. A circle graph is usually used to easily show the results of an investigation in a proportional manner.
We can apply the Intersecting Chords Theorem. We investigate the relationship between the side lengths of a right triangle. The reference number associated with t is the shortest distance along the unit circle between the terminal point determined by t and the x-axis.
This section explains circle theorem including tangents sectors angles and proofs. You should try to remember sin. A circle is the same as 360.
When to Use Law of Sines vs Cosines. So we can use Rule 7 the angle in a semi-circle is a right-angle to deduce that angle BAD 90degree. The indirect reasoning is embodied in a theorem frequently called the Squeeze Theorem.
One of the best known mathematical formulas is Pythagorean Theorem which provides us with the relationship between the sides in a right triangle. Begingroup Masons were not obligated to use compass and straight edge according to the rules of Euclidian geometry. The two legs meet at a 90 angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.
The video below highlights the rules you need to remember to work out circle theorems. X 2 y 2 1 2. The key point to take from these examples is that an accumulation function is increasing precisely when is positive and is decreasing precisely when is negative.
The demonstration also illustrates what happens when the sum of 1 pair of sides equals the length of the third side--you end up with a straight line. Equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constantThe distance between any point of the circle and the centre is called the radiusThis article is about circles in Euclidean geometry and in particular. We would like to show you a description here but the site wont allow us.
Let be a continuous function on the real numbers and consider From our previous work we know that is increasing when is positive. Also since xcos and ysin we get.

Circle Theorems Maths Numeracy Educational School Posters Circle Theorems Studying Math Math Poster
Eight Circle Theorems Page

Circle Theroms Maths Questions Worksheets And Revision Mme

Maths Desk Prompts Circle Theorems Desk Mat
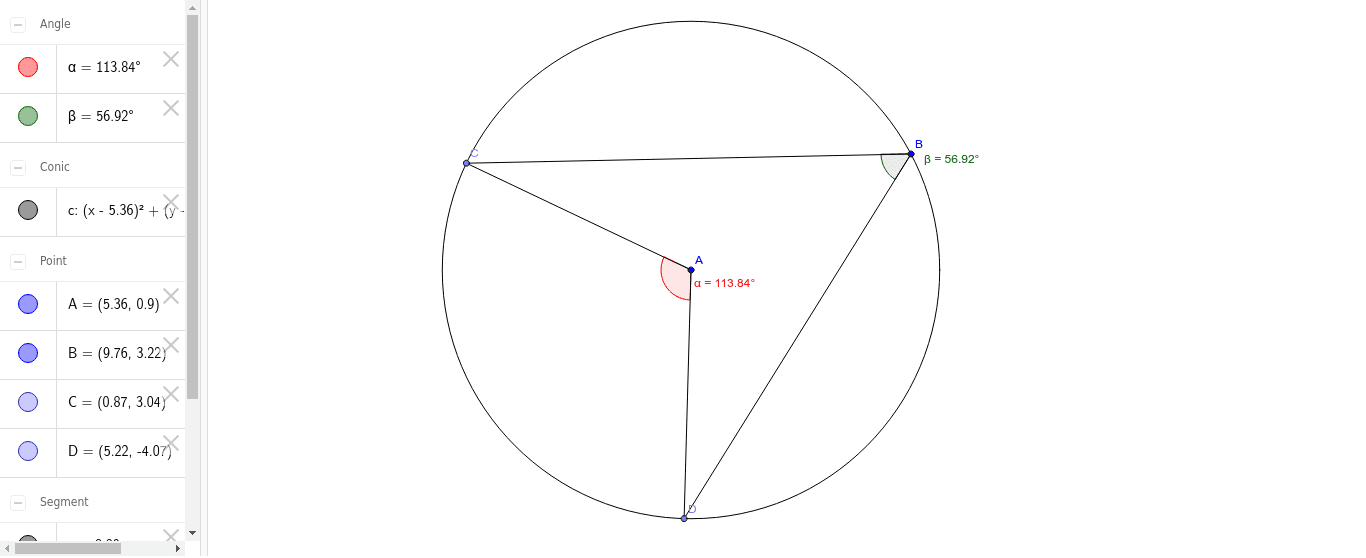
Circle Theorems Arrowhead Rule Geogebra
Circle Theorems Mathematics Gcse Revision

Circle Theorems Revision Ks4 Maths Teachit
Eight Circle Theorems Page

