We call this a triple zero or a zero with multiplicity 3. Plotting points Transformation how to graph of cubic functions by plotting points how to graph cubic functions of the form y ax h3 k Cubic Function Calculator How to graph cubic functions using end behavior inverted cubic vertical shift horizontal shift combined shifts vertical stretch with video lessons examples and step-by-step solutions.
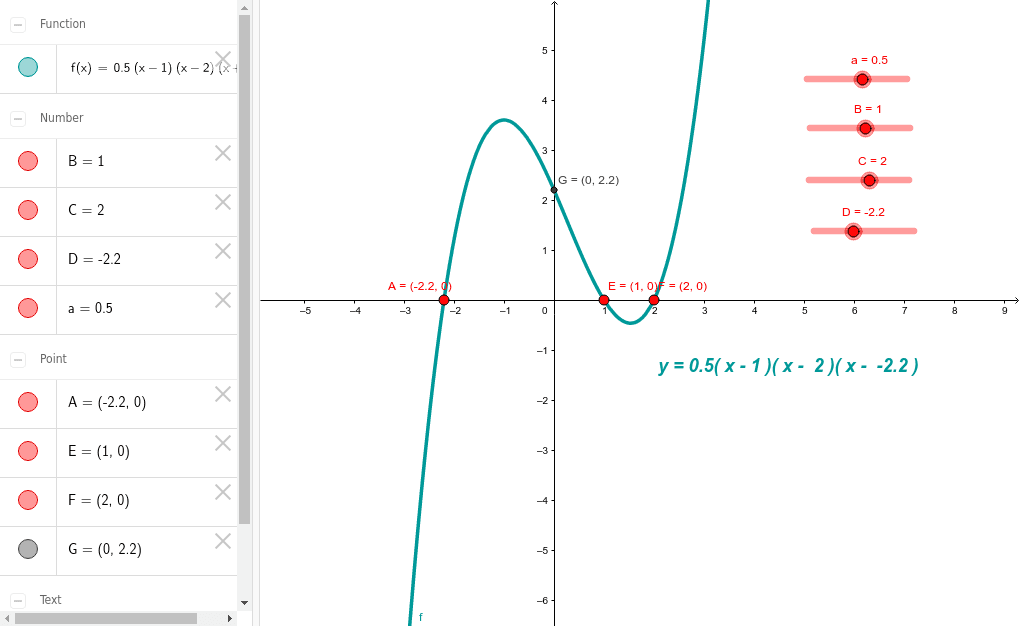
Exploring Cubic Graphs Geogebra
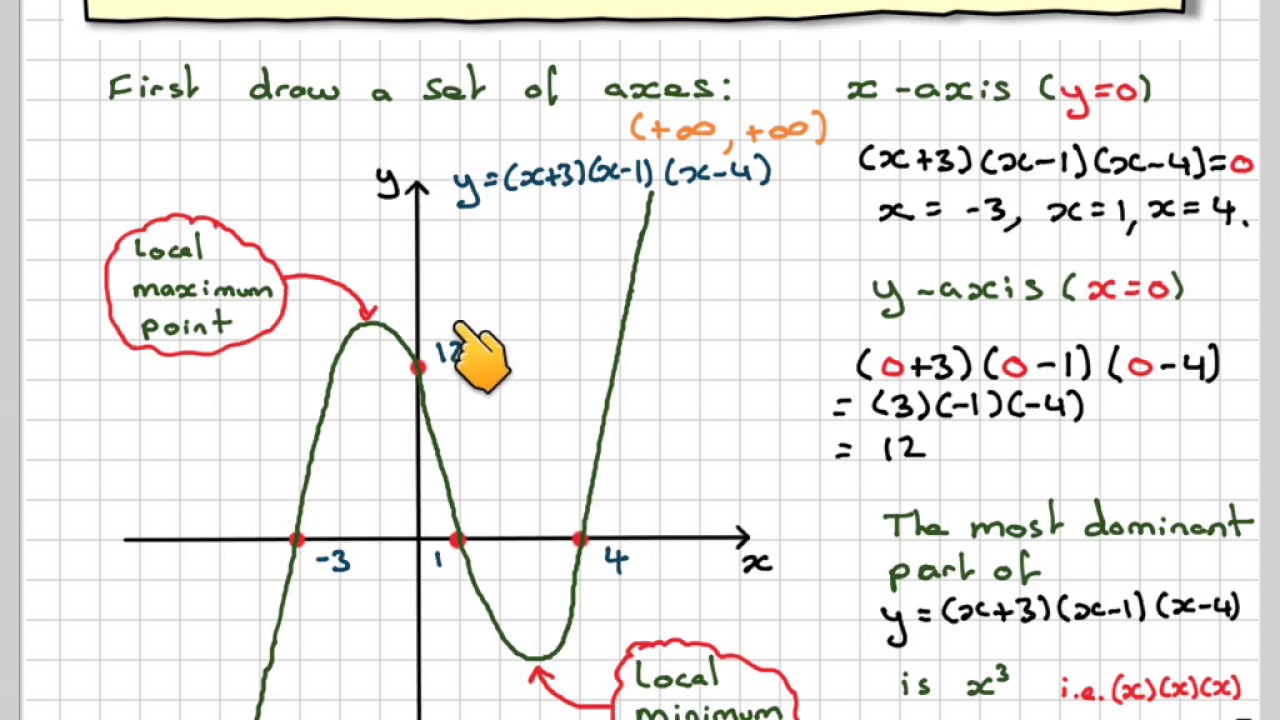
Sketching The Graph Of A Cubic Function 01 Youtube
Can You Please Help Me With X Y Tending To Infinity With Sketching Cubic Graphs The Student Room
For zeros with even multiplicities the graphs touch or are tangent to the x-axis.
How to sketch cubic graphs. Curved Graphs This worksheet is designed to cover one question of each type seen in past papers. A line a curve or a region. Find the x and y intercepts of the graph of f.
Understanding these translations will allow us to quickly recognize and sketch a new function without having to resort to plotting points. This factor is cubic degree 3 so the behavior near the intercept is like that of a cubicwith the same S-shape near the intercept as the toolkit function f x x 3. The function fxx33x24x is a cubic function.
A - The y intercept is given by 0 f0 0 0 The x coordinates of the x intercepts are the solutions to x 3 0 The x intercept are at the points 0 0. To use the remainder theorem and the factor theorem to solve cubic equations. For each function we will look at efficient ways to sketch the graph discuss domain and range and make observations about some features of each graph.
The graphs of reciprocal functions are made up of branches which are the two main parts of the graph. In this module we look at the graphs of five base functions. Find the horizontal and vertical asymptotes of the graph of the function 2 1 3 6 x f x x.
This factor is cubic degree 3 so the behavior near the intercept is like that of a cubicwith the same S-shape near the intercept as the toolkit function We call this a triple zero or a zero with multiplicity 3. For zeros with even multiplicities the graphs touch or are tangent to the x-x-axis. Explore the definition formula and examples of a cubic function and learn how to solve and graph cubic functions.
Changes to the equation cause changes to the shape and that the nature of these changes is consistent across different types of graphs. Match up the sketch with the function. Graphing of Cubic Functions.
We can use what we have learned about multiplicities end behavior and turning points to sketch graphs of polynomial functions. 0 x y y 0 x Mathematics Learning Centre University of Sydney 2 112 The Vertical Line Test The Vertical Line Test states that if it is not possible to draw a vertical line through a graph so that it cuts the graph in more than one point then the graph is a function. Quadratic cubic and reciprocal graphs Differentiated lesson that covers all three graph types - recognising their shapes and plotting from a table of values.
We call this a triple zero or a zero with multiplicity 3. To sketch the graph of fuse the information from your previous answers and combine it with the fact that the graph is a parabola opening downward. For students to complete a detailed sketch.
Symmetry in Polynomials Similarly it should follow that even polynomial functions would have only even degree terms. Higher GCSE recognising graphs cut and stick. By understanding the basic graphs and the way translations apply to them we will recognize each new graph as a small variation in an old one not as a completely different graph that we have never seen before.
This factor is cubic degree 3 so the behavior near the intercept is like that of a cubic with the same S-shape near the intercept as the function latexfleftxrightx3latex. F x x 3. We call this a triple zero or a zero with multiplicity 3.
Graph and compare features of the graphs of cubic equations of the form. And asymptotes which are horizontal and vertical lines that the graph approaches but doesnt. Y a x - r x - s x - t describe interpret and sketch.
Starter task requires students to sketch linear graphs from a table of values. Sketch the graph of the function y 214 81-2. The quadratic function the square root function the reciprocal function the exponential function and the absolute value function.
Find the domain and range of f. Find the intercepts if possible. In Quick Sketch students will recall consolidate and develop the following essential skills.
For zeros with even multiplicities the graphs touch or are tangent to the x-axis. Determines the midpoint gradient and length of an interval and graphs linear relationships MA51-6NA. To find equations for given cubic graphs.
F x x 3. To state that The pressure drop across the column in inches of water was plotted on log-log coordinates as a function of air flow rate in cubic feet per minute. The plot shown in Figure 3 was close to linear and the slope of the best straight line 192 was close to 2 as predicted by theory.
Two sketches left blank for the student to complete. Solution to Example 1. 21 3 x3 21 213 2r2.
Let us put this all together and look at the steps required to graph polynomial functions. Recognize the typical shapes of the graphs of polynomials of degree up to 4 understand what is meant by the multiplicity of a root of a polynomial sketch the graph of a polynomial given its expression as a product of linear factors. F is a cubic function given by f x x 3.
Form and graphing worksheet answer key features of the equation in the first time. For zeros with even multiplicities the graphs touch or are tangent to the x-axis. Sketch the graph of f.
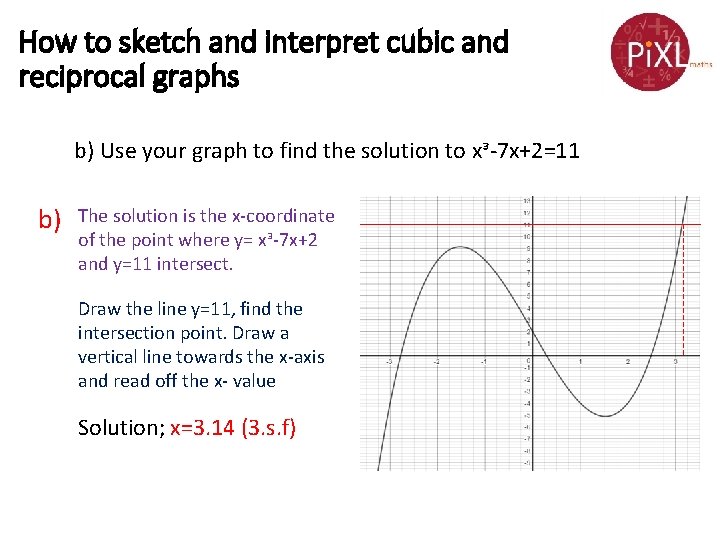
Sketch the graph of a function in neighborhood x2 that satisfies these conditions f23 f22 f2-1 you can find a specific function that satisfies all of the given conditions i know the first derivative gives you critical points and secondClick here to see ALL problems on Graphs. Cubic graphs and their equations worksheet answers In this worksheet we will rehearse the graph of cubic equations and use this graph to find its solution or solutions. Linear quadratic cubic and reciprocal graph.
Given a polynomial function sketch the graph. Complete a table of values for a cubic or quadratic equation for. This factor is cubic degree 3 so the behavior near the intercept is like that of a cubicwith the same S-shape near the intercept as the toolkit function f x x 3.
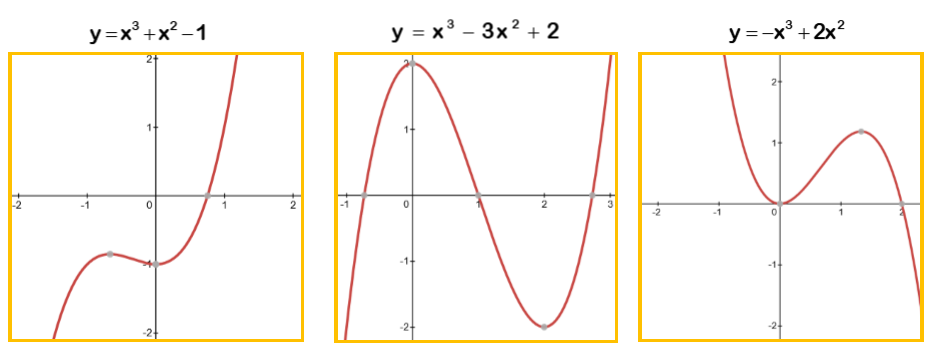
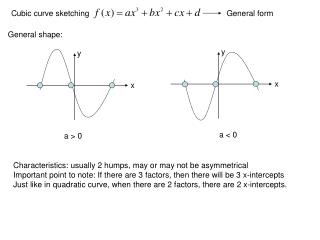
Consider the following cubic functions and their graphs. Cubic and Quartic Functions Objectives To recognise and sketch the graphs of cubic and quartic functions. All equations describe a shape.
A cubic function is a third-degree function that has one or three real roots. Here we learn how to sketch graphs of cubic functions which are composed of linear factors and repeated factors.
Cubic Graphs Worksheets New Engaging Cazoomy

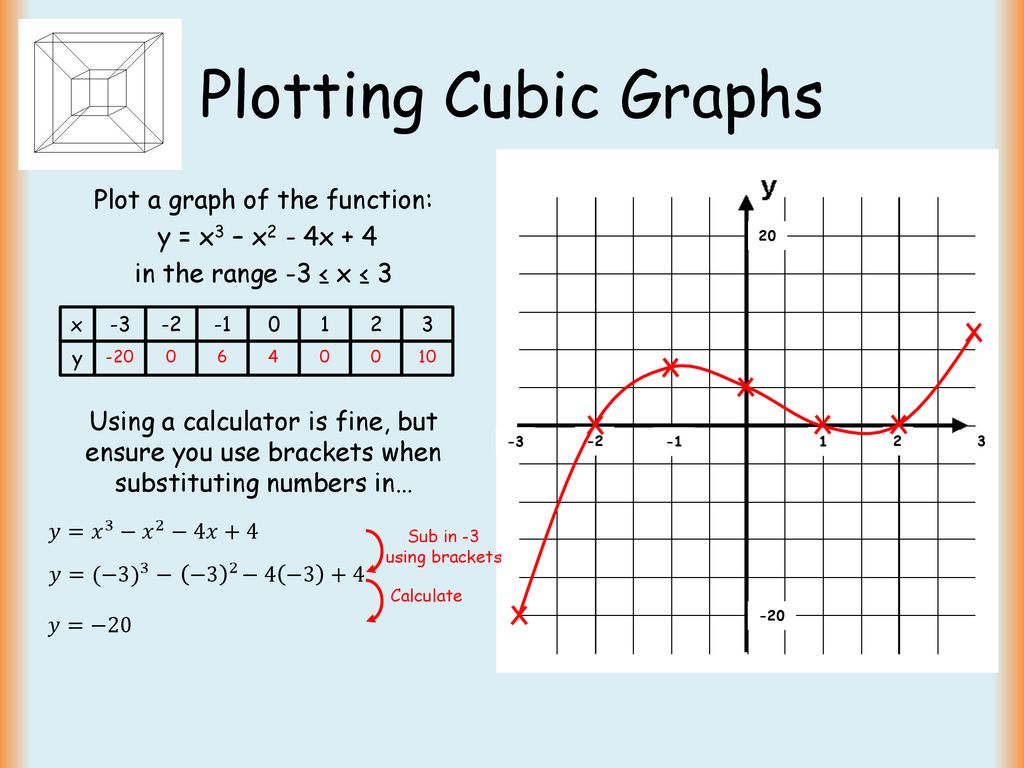
Plotting Cubic Graphs Ppt Download
Grade A Cubic And Reciprocal Functions Recognise Sketch

Algebra Graphs Cubic Graphs Ssdd Problems

Sketching Cubic Graphs Differential Calculus

Example Sketching A Cubic Function Youtube

Graphing Cubic Functions
Ppt Cubic Curve Sketching Powerpoint Presentation Free Download Id 1030663
- Android App Image
- Beta Ray Bill Ragnarok
- Taman Camar Kulim
- Watson Batu Gajah
- Design Baju Nikah Simple
- How To Monetize Copyrighted Music On Youtube
- Lirik Gerhana Cinta Luka
- I Love You In Tamil
- Kedai Kek Kulim
- Star Wars Jedi Fallen Order
- How To Blink Cell In Excel
- Glass Bottle Quality Standards
- Poskod Tasek Gelugor
- undefined
- Hidden Door Mirror
- How To Turn Off Google Chrome Ad Blocker
- Cross Channel Messaging
- Klinik Gigi Paka
- 鲍 一 凡
- English To Korean Google Translate

